关于通信原理的一点总结

abc_leo

学了通信原理这门课，一开始觉得很难，而且听学长们也总是告诫大家，通信原理是很难的课程，平时一定要好好学，不然自己复习的日子根本就抓不到要点了。事实上好像也是如此，在周围，这门主课的挂课率总是算前排的。当然对于我这样的人，总是上课时算是比较认真的，但是半期的时候还是没有搞懂它是干什么的，甚至到期末了，也只有零星的一点编码呀，带宽呀，调制啦，这样一些概念，但这些技术在一个通信系统中又是出于什么样的位置，该怎样应用这些技术组成一个通信系统，对此我还是一概不知。然而经过期末前的复习，我感觉自己对通信系统总算有个印象了，所以想把那些零碎的名词做一些说明，并且用我自己的学习过程以及对通信系统的了解来说明这些技术的应用。

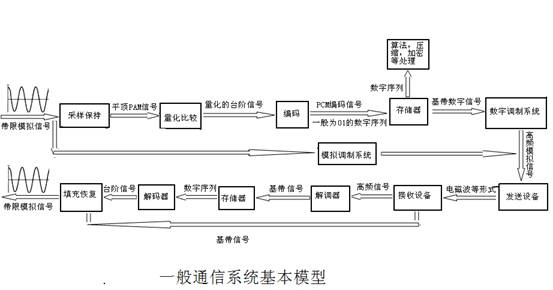
上面是我画的认为比较完整的通信系统的简单流程图，对此我做一翻说明。

首先日常生活中的信号总是模拟的，大家把这些信号通过滤波等处理，得到带限的信号，这里以基带信号singnal为例子,signal 经过采样保持电路，大家就得到PAM信号，如图

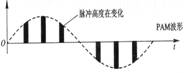
，这样的信号就是离散信号了。

离散信号经过量化归属到个档次的幅度中比如大家有2V,4V,6,V,8V四个档次的归类，并且规定1V~3V之间的PAM离散信号就归类到2V的档次中去,一次类推，通过比较给每个PAM信号进行归类，这就是量化。

之后将量化了的信号进行编码，编码是一种认为规定的过程比如大家规定2V用00表示，4V用01表示，6V用10表示，而8V用11来表示,这样就把阶梯信号和二进制信号有了一种对应关系，顺着这种对应关系，大家可以得到刚才量化了的信号的二进制代码，这就是PCM编码得到了可以在存储器中存储的数字信号。

以上从模拟到数字信号的一种转变就是大家常说的A/D转换。至于大家平时要求的转换比特率的求法可以从它的转换过程得出计算方法。一个PAM信号对应一个档次，而一个档次对应几个比特的数字是在编码中体现的，例子中就是一个档次对应两个比特，假设这种对应关系是1对N个比特，对模拟信号的采样率是F,也就是1秒钟有F个PAM信号，这F个PAM信号就要被转换成F*N个比特，所以比特率就是F*N了。

对于完成转换的数字信号，大家如何处理呢？有的是被放进存储器中存储了，有的是到CPU中进行计算，加密等处理了。

通常为了达到通信目的，大家就要将数字信号传递并且转换成模拟信号，毕竟在生活中模拟信号才是大家可以识别的。

所以大家从存储器中读取数字信号，这些信号是基带信号，不容易传输，经过数字调制系统就可以转换成高频信号而被发送设备以各种形式比如微波，光信号传播出去。发送这些高频信号的速度关系到发送的比特率注意与前面的转换的比特率有不同。假如整个发送端可以发送四中波形A,B,C,D，它们可以分别表示发送了00，01，10，11信号，那么大家就说发送一个符号（即波形）就是发送了两个比特了。由此得到符号率与比特率的关系B=N*D.D是符号率baud/s, B是比特率bit/s, N表示一个符号与N个比特对应。

接收设备将这些信号转换成电信号，通过解调器，就可以还原基带信号，同样可以将它们放进存储器存储，这可以理解成网络视频在大家的电脑上的缓存。缓存中的信号通过解码器，也就是与编码器功能相反的器件将数字序列转换成各种量化的台阶（档次）信号。

最后将台阶信号进行填充恢复，大家就又可以原来的输入的模拟波形了，由此大家完成一次通信。

如果模拟信号不需要数字化，那么大家可以进行模拟调制，同样可以发送出去，这个过程要简单很多。

当然，这里所讲的只是大家学习中所涉及的一些概念，完整的通信系统还有更多要考虑的，这只是我觉得通信过程的关键的骨架问题。

还有几个概念是对它们的理解和总结，希翼可以和大家分享。

1. 二进制比特率与信息量中的比特率。

因为大家假定二进制信号是等概率发生的，也就是P=0.5，而信息量的定义是这样的I=-log2(p)bit,通过此式，大家可以计算发送的一个二进制符号的信息量I=-log2(0.5)bit=1 bit,所以大家通常说一个0或者1就是一个比特了。

2. 方波的带宽问题。

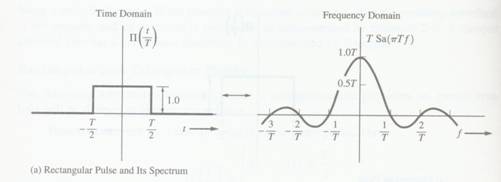
由上图大家可以注意到，一个持续时间为T的方波，它的频谱是一个SINC函数，零点带宽是1/T，即时间的倒数。当然，方波的带宽是无限大的，因此这样的波形在现实中是很难实现的，大家只能给方波提供一定的带宽，就是说得到的肯定只能是经过了过滤的波形。

在这里大家可以联系到吉布斯现象。大家可以这样理解：频率越大，就说明变化越快，而方波的转折点处就是一个极快的变化也就是有频带的高频部分构成，而经过带限的滤波之后，高频被滤去，得到的波形在转折点处就变化慢下来，于是在需要变化快的地方（如方波的转折点）变化慢，由此产生吉布斯现象。   

3. 升余弦滚降滤波器。

大家知道升余弦滚降滤波器是防止码间串扰而设计的。码间串扰是指各个时间点上发送的符号并非准确的方波，而是在规定的时间内仍有余波，于是对下一个时刻发送的符号产生影响，最后可能因为影响的叠加效果而使后果严重，得到相反的采样结果。注意大家这里讲的码间串扰都是发生在基带频率上的。因此升余弦滚降滤波器也是在基带上的应用。

下图是升余弦滚降滤波器的原理图，上半部分是滤波器的频谱相应图，下半部分是滤波结果在时间域上的波形图。

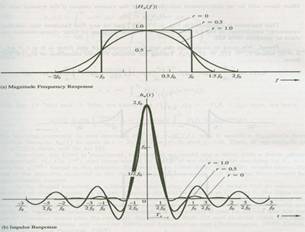
大家可以这样思考，发送的基带波形是在一定的带限内的，假如说要求发送的符号率是D，那么图下半部分中可知1/2f0=1/D，所以f0=1/(2*D),或者说D=2* f0,由下半图大家可以看出大家发送的符号的频率是2* f0，这串符号在频谱上的表示（上半图）是个带宽为f0的信号，这个就是采样定理中说的当波形用SINC函数来表示时，符号率是该波形的带宽的两倍，也就是升余弦滚降滤波器在r=0的时候的特性。

当然，大家这里表示的只是发送一个符号的波形的带宽，但是大家可以这样想象，一个系统在任何时候发送符号是使用的带宽f0都是固定的，在1时间段内发送的波形的带宽在f0以内，那么大家完全有理由相信在2时间段内发送的波形的带宽必然在f0以内，所以这样可以理解多个符号组成的波形的带宽是在f0以内的。

从下半图大家可以看到，随着r的增加，符号波形在一个周期段以外的衰减就会加快，这里大家就可以看到它对码间串扰的影响会减小，这个就是升余弦滚降滤波器的作用，但是大家必须清楚的看到，符号率是不变的2* f0,而系统的绝对带宽在增加。根据升余弦滚降滤波器的定义大家得到这样一个关系D=2* f0/(1+r)。从以上的分析过程大家可以认为1/2*f0就是发送的数字信号的周期，也就是对于同样周期的信号大家需要不同的带宽，这个带宽就是发送的数字信号的带宽，而与原始的模拟波的带宽无关。

4. 调制的一些想法。

在学习调制的过程中，我一直搞不清什么是调制信号，什么是载波。最后总算明白，原来（一般来讲）调制就是将低频信号（调制信号）携带的信息在另外一个高频的信号（载波）上表现出来，表现的方法可以是改变载波的幅度或者相位或者频率等。当大家看到调制完成的波形是，发现它与载波有不同的幅度或者相位或者频率，从这里的变化大家极可以判断处调制信号有那些信息。载波就是用来携带低频信号要表达的意思的高频信号。之所以用高频是因为在一般情况下高频信号便于传输。

以上是我在学习通信原理中觉得关键要明白的只是点，这样常识才可以融会贯通。